This is a guest post written by Snehlata Sharma. Snehlatha completed her MSc, MEd in Mathematics. She has been teaching mathematics for over 18 years. She has a deep understanding of important mathematical skills and teaches students by using unique teaching techniques that help them to understand mathematics concepts easily and efficiently. These shortcut methods and techniques save a lot of time in exams. Do subscribe to Snehlata Sharma YouTube Channel for latest updates.
This video contains basic concepts of a pair of linear equations in two variables and algebraic methods of solving them. From this video we will learn how to solve a pair of linear equations in two variables using most commonly used algebraic methods like substitution method, elimination method and cross-multiplication method. We shall also study about the application of linear equations in two variables in solving simple problems from different areas. These are very useful Maths tricks for 10th CBSE and State Board Exams and also useful for other competitive exams.
Pair of Linear Equation in Two Variables
Linear equation is of the form ax + by + c = 0
If two linear equations have two same variables, then they are called a pair of linear equations in two variables. Following is the most general form of pair of linear equations in two variables:
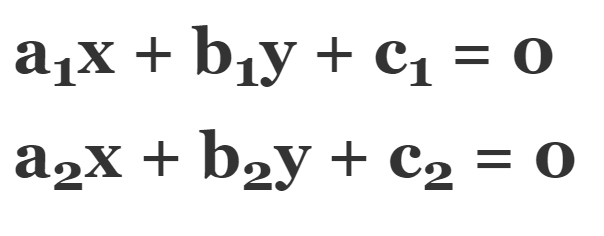
Here, a1, a2, b1, b2, and c1, c2 are real numbers such that:
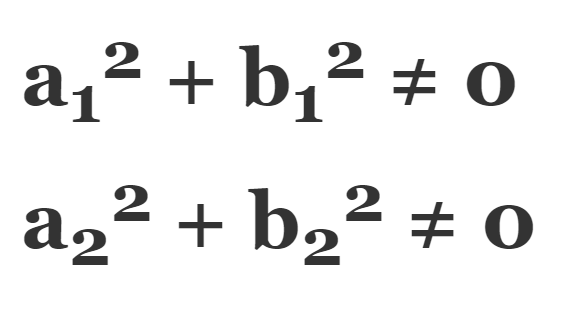
There are basically two types of methods of solving linear equations in two variables:
- Graphical Method
- Algebraic Method
Graphical Method of Solving a Pair of Linear Equations in Two Variables
In Graphical Method we will be drawing graphs of two equations and intersection point is called the solution of the graph. We all know that a graphical representation of a linear equation in two variables is a straight line and when we have a pair of linear equations the following cases arises:
1). When the real numbers a1/a2 ≠ b1/b2 we say that the lines intersect at a point and this point gives us the unique solution of the two equations. In this case the pair of linear equations is consistent and we have a unique solution.
2). Second case arises when these real numbers a1/a2 = b1/b2 ≠ c1/c2
In this case the lines are parallel and the pair of equations has no solution. This means the two straight lines represented by their linear equations will meet nowhere so there is no solution and the system is called inconsistent.
3). Third case arises when a1/a2 = b1/b2 = c1/c2
In this case the lines coincide with each other. The second line is overlapping over the first line. Because they coincide each other, the pair of linear equations have infinite many solutions. As all the points on the lines are the point of intersection we can say that it has infinite solutions. And for these equations we say that they are dependent on each other and they are called consistent system.
To solve a pair of linear equations in two variables we have two methods as we have discussed above. The first method is graphical method and the second method is algebraic method. In graphical method we will draw the graph of each of the linear equations and find the point of intersection of that graph and that point of intersection will give us the solution. But this method is not convenient because in some of the cases the point representing the solution of linear equation has non integral values like they may intersect at the point (2.37, -4.19) and this may be the one of the solution of the linear equation. So it gives us the inappropriate values of x and y where as the algebraic method provide us the exact and the correct solution of every pair of linear equations.
Algebraic Methods of Solving a Pair of Linear Equations in Two Variables
In the Algebraic Method there are many methods. The most commonly used Algebraic Methods of solving a pair of linear equations in two variables are as follows and we will discuss them one by one:
- Substitution Method
- Elimination Method
- Cross-Multiplication Method
Substitution Method of Solving a Pair of Linear Equations in Two Variables
Let us start with Substitution Method first. Let us consider the example, we have a system of linear equations:
- 2x + 2y = 10
- 3x – 3y = 16
We are solving these two equations by Substitution Method. For Substitution Method we will find out the value of one of the two variables x or y in terms of the other from these two given equations and then substitute this value in the other equation and this will give us a linear equation in one variable and we will solve that linear equation in one variable to find the value of x, y. So let us start.
Let us start from the first equation 2x + 2y = 10
We have 2x = 10 – 2y
x = (10 – 2y)/2 if we take 2 outside this will take the form x = 5-y
Now we will put this value of x in the second equation 3x – 3y = 16 to get the value of y.
Now from second equation 3x – 3y = 16 substituting the value of x we have:
3 (5 – y) – 3y = 16
15 – 3y – 3y = 16
So this is -6y = 1
The value of y is -1/6
Now we will substitute this value of y in the equation x = 5 – y
So x = 5 + 1/6 = 31/6
Therefore solution of the two linear equations 2x + 2y = 10 and 3x – 3y = 16 are x = 31/6 and y = -1/6
These are the required solution of these pair of linear equations in two variables.
Elimination Method for Solving a Pair of Linear Equations in Two Variables
Now we will solve the same pair of linear equations in two variables by Elimination Method. Let us discuss elimination method for solving this pair of linear equations 2x + 2y = 10 and 3x – 3y = 16. For this elimination method we will multiply the given equations by suitable non-zero real number so as to make the coefficient of any of the variable numerically equal in both the equations and after that we will add or subtract the new equation so obtained to eliminate one variable from both the equations whose coefficients are numerically equal and after that we will solve the simple equation in one variable thus obtained.
So by looking at the two equations we can see that if we make the coefficient of x as 6 in the first equation and to make the coefficient of x is equal to 6 in the second equation, we will multiply the whole second equation by 2 and to make the coefficient of x = 6 in the first equation we will multiply whole first equation by 3.
So after multiplying, the two equations 2x + 2y = 10 and 3x – 3y = 16 becomes 6x + 6y = 30 and 6x – 6y = 32
Now we have two equations in which the coefficients are same and if we add these two equations we can easily eliminate the Y variable. So let us add. If we add these two equations it will become 12x = 62. So value of x = 62/12 = 31/6
If we substitute this value of x in any of the two equations we can easily get the value of y.
Now substituting this value of x in the first equation 2x + 2y = 10 we will get 2y = -1/3 and value of y = -1/6
So the required solution is:
x = 31/6
y = -1/6
Cross-Multiplication Method of Solving a Pair of Linear Equations in Two Variables
Now we will discuss the cross-multiplication method. Our pair of linear equations in two variables are:
2x + 2y = 10
3x – 3y = 16
Let me tell you an easy way of solving the problems by cross multiplication method. For cross multiplication method we have the formula: 
The downward arrow indicates the first product while the upward arrow indicates the second product. The second product is to be subtracted from the first product. Since the denominator has been obtained by the cross multiplying the coefficients this method is known as method of cross-multiplication for solving a system of linear equations.
For this particular question we have b1 = 2, b2 = – 3, c1 = 10, c2 = 16, a1 = 2, a2 = 3
After cross-multiplication according to the above formula we will get x/62 = y/-2 = 1/12
Therefore value of x = 31/6 and value of y = -1/6
So we have the same solution whatever may be the method. Whether it is Substitution Method, Elimination Method or Cross-Multiplication Method our answer remains the same. For this particular question by cross multiplication method we got x = 31/6 and y = -1/6 and the same solution we got in all the three types of method.
I hope you understood all these algebraic methods of solving a pair of linear equations in two variables clearly. If you have any doubts you can write in below comment box.