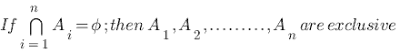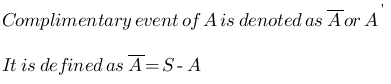Random Experiment or Trail
An experiment which satisfies the following conditions is called as a random experiment.
- It can be conducted several number of times under similar conditions.
- The list of all the outcomes of the experiment must be known.
- The result of the experiment is uncertain.
For example: tossing a coin, rolling a symmetric dye, drawing a card from a well shuffled pack of cards etc.
Simple Events
Each outcome of a random experiment is called a simple event.
Sample Space
A set of sample events of a random experiment is called a sample space.
Event
Every subset of the sample space of a random experiment is called as an event.
For example, if we consider an experiment of drawing a card from a well shuffled pack of cards, “getting a king card” is an event whereas getting a spate king is a simple event.
Impossible and Certain Events
If ‘S’ is the sample space then Φ, s are subsets of S. Φ is called impossible event and s is called certain event. That is, an event which has no chance of occurring is called as impossible event and an event which always occurs is called as a certain event.
The important point to note here is – If the sample space has n-simple events then the total number of events that may occur is 2 to the power of n (2n).
Exclusive Events
If two events are disjoint in the sample space then they are called as exclusive events. That is, if the happening of one event restricts the happening of the other then the events are said to be exclusive.
Mutually or Pairwise Exclusive Events
A1, A2, A3,………, An are said to be mutually exclusive if and only if
Exhaustive Events
If the union of the given events is the sample space, then they are called as exhaustive events. That is whenever the experiment is conducted if we get one of the given events always then the given events are called as exhaustive events.
If for the events, A1, A2, A3,………,An union of all these events equals sample space then all the events are called exhaustive events.
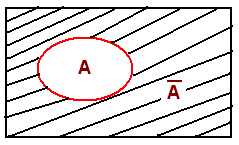
Complimentary Event
S is a sample space, A is any event, then the event S-A is called or defined as complimentary event of A and is denoted and defined as follows:
Note that both both ‘A’ and ‘Complementary event of ‘A’ are exclusive & exhaustive events.