Define Adjoint of a Matrix

Adjoint of a Matrix

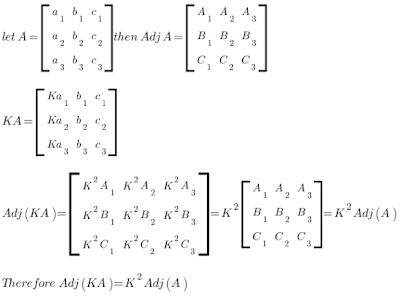
If A is a square matrix then the transpose of a matrix obtained by replacing the elements of A by their co-factors is called the adjoint of a matrix A and is denoted by Adj A. For example,

Note

1. 
2. If A is a square matrix of order ‘3’ and K is any scalar then Adj (KA) = K^2 Adj A
   

   Proof :-

   

   Likewise, If A is square matrix of order ‘n’ then Adjoint of KA = K to the power of (n-1) times Adjoint of A