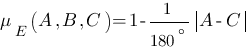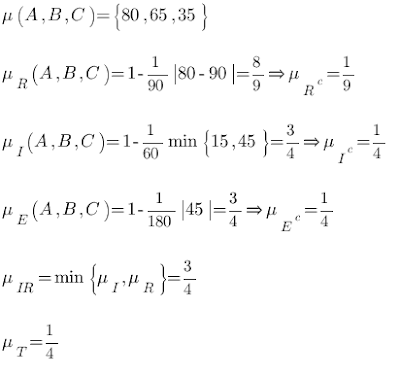Intuition
This method needs no introduction. It is simply derived from the capacity of human to develop membership functions through their own innate intelligence and understanding.
Inference
In inference method we use knowledge to perform deductive reasoning. To deduce or infer a conclusion, we have to use the facts and knowledge on that particular problem. Let us consider the example of Geometric shapes for the identification of a triangle.
Let A, B, C be the interior angles of a triangle such that
A ≥ B ≥ C > 0° and A + B + C = 180°
For this purpose we are having or defining 5 types of triangles namely:
- R = Approximately Right-Angle Triangle
- I = Approximately Isosceles Triangle
- E = Approximately Equilateral Triangle
- I.R = Isosceles Right-Angle Triangle
- T = Other type of Triangle
Now we can infer membership values for all those type of triangles through the method of inference because we posses the knowledge about the geometry of their shapes for assigning membership values. Below given are the membership values for the 5 types of triangles defined above.