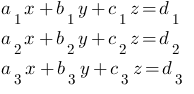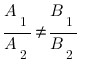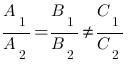Matrices EAMCET Part 2 – Homogeneous Equations and Non-Homogeneous System

Go here for Matrices EAMCET Part 1

Homogeneous Equations

If the system is AX=0 and

1. |A| ≠ 0 then the system has unique solution, that is the zero solution.
2. |A| = 0 then the system has atleast 1 non-zero solution. In-fact the system has infinite number of solutions.
3. If the number of equations in a homogeneous system is less than number of unknowns then system has infinite number of solutions.

Non-Homogeneous System

Suppose the given non-homogeneous system is AX = B, find Δ, Δ1, Δ2, Δ3 and

1. If Δ ≠ 0 the system has unique solution . In the above case the given equations represent three planes intersecting in a point.
   
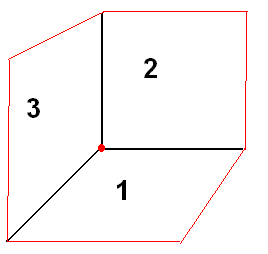
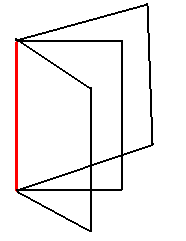
2. If Δ = 0, Δ1 ≠ 0, ( Δ2, Δ3 = 0) then the system has no solution. In this case the given equations represent three planes forming a triangular prism or parallel planes, not coincidental.
   

     

   
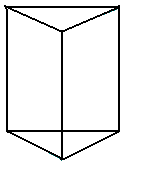
3. If Δ= 0, Δ1 = 0 ( Δ2, Δ3 = 0), then the system has infinite number of solutions. In this case the given equations represent three planes passing through a line or a coincidental planes.
   

Suppose the given non-homogeneous system is

Consider two pairs of the above equations eliminate the same unknown. Suppose the equations thus obtained are

when z is eliminated.

1. If
   
2. If
   

   then the system has no solutions.

3. If