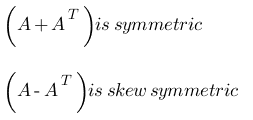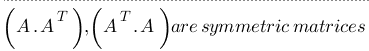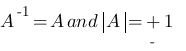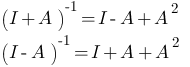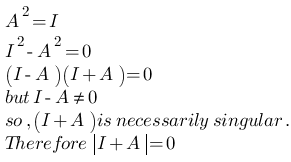Matrices EAMCET – Part 1

Here are some of the most important points from matrices to be understood and remembered by EAMCET aspirants.

1. Product of two upper triangular matrices is a upper triangular matrix.
2. Determinant of triangular matrix is the product of the elements in the principle diagonal.
3. (i) trace (KA) = K tr(A)
   (ii) tr (A + B) = tr(A) + tr(B)
   (iii) tr (AB) = tr (BA)
4. If A is a skew symmetric matrix then,
   1-> All the elements in the principle diagonal are equal to zero.
   2-> |A|≠ 0 then its order is an odd number.
5. If A, B are symmetric matrices, K is a scalar then
   (i) KA is symmetric.
   (ii) (A + B) and (A – B) are symmetric.
   (iii) AB, BA are symmetric if and only if AB = BA.
6. For any square matrix A, (A + A^T) is symmetric and (A – A^T) is skew symmetric.
   
7. A is a matrix of order m x n then A.A^T, A^T.A are symmetric matrices.
   
8. The only non-singular idempotent matrix is the unit matrix. That is if A² = A and A ≠ I then |A| = 0
   
9. If A, B are square matrices of the same type satisfying the condition AB = A, BA = B then
   (i) Both A and B are idempotent matrices
   (ii) For any natural number ‘n’, (A+B)ⁿ = 2^(n-1) (A+B)
   
10. If A is an involutary matrix then,
    
11. If A is an orthogonal matrix then,
    

    Determinant of A is ±1. If the rays are in right handed system then the value of determinant is +1 and if they are in left handed system then the value is -1.

12. Every nilpotent matrix is a singular matrix.
13. If A is a nilpotent matrix of index 3 then,
    
14. If A is involutary matrix and A ≠ I, then the determinant of |I + A| = 0.
    Proof :-