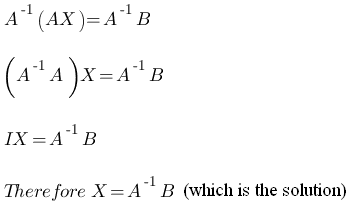Non-Homogeneous Linear Equations:-
a1 x + b1 y + c1 z = d1
a2 x + b2 y + c2 z = d2
a3 x + b3 y + c3 z = d3 is called a system of non-zero homogeneous linear equations.
then it can be written as AX = B where A is called co-efficient matrix.
Consistent and Inconsistent System :-
If a system of linear equations has a solution then the system is said to be consistent. Otherwise it is said to be inconsistent system.
Different Methods to Solve Non-Homogeneous System :-
The different methods to solve non-homogeneous system are as follows:
- Matrix Inversion Method :-
Suppose the given system is AX = B and A is non-singular then inverse of A exists. - Cramer’s Rule :- Suppose the given system is
a1 x + b1 y + c1 z = d1
a2 x + b2 y + c2 z = d2
a3 x + b3 y + c3 z = d3 and Δ, Δ1, Δ2, Δ3 are as given below, then by multiplying the equations with A1, A2, A3 and then by adding we get x(a1A1 + a2A2 + a3A3) + y(b1A1 + b2A2 + b3A3) + z(c1A1 + c2A2 + c3A3) = d1A1 + d2A2 + d3A3x.Δ + y.0 + z.0 = Δ1 -> x = Δ1 / Δ
Similarly multiplying the equations with B1, B2, B3 and then by adding we get y = Δ2 / Δ and by multiplying C1, C2, C3 and by adding we get z = Δ3 / Δ.
- Gauss Jordan Method : For this method elementary row transformations are done. The following are called elementary row transformations:
1-> Interchange the two rows.
2-> Multiplication of a row with a non-zero constant K.
3-> Addition of products of elements of a row and a constant K to the corresponding elements of some other row.
Augmented Matrix :-
For the non-homogeneous linear system AX = B, the following matrix is called as augmented matrix.
Working Rule :-
Suppose the given system is
a1 x + b1 y + c1 z + d1 = 0
a2 x + b2 y + c2 z + d2 = 0
a3 x + b3 y + c3 z + d3 = 0
By applying the elementary row transformation we have to transfer the Augmented matrix into the standard solution form as given below after which we can the solution as x = α | y = β | z = γ